What is Measurement Uncertainty
There is an uncertainty associated with every test and calibration. For testing, this occurs from errors arising at the various stages of sampling, sample preparation, measurement and data evaluation. In other words, whenever any quantitative measurement is performed, the value obtained is only an approximation of the true value. Users of the measurement data should have an idea of how much the reported result may deviate from the true value.
ISO/IEC 17025 recommends the results of quantitative measurement to be reported as both a single value and together with the possible deviation from the true value. This is logical for any report with quantitative results. It is, for example, of no use if a report on a food sample states 0.1 percent of compound X, and the user of the data is still unsure whether this could be 0.05 or 0.4 percent. An uncertainty statement provides the user with information on the approximate measurement tolerances and the expected limits within which the true value of the measurement, such as analytic concentration, is supposed to lie. Without such documentation, although the analyst can estimate the level of uncertainty many times, the client or user of the data cannot.
Information on uncertainty is of particular importance if a specification limit is to be verified and reported. For example, if according to a purchasing agreement, a product can only be released if compound X is below 0.5 percent, the test report may not contain a statement about compliance if the measurement results extended by the measurement uncertainty is above 0.5 percent. When parameter(s) are claimed to be within a specified tolerance the measurement value(s) extended by the estimated uncertainty of measurement shall fall within the specification limit.
ISO has published a Guide to the Expression of Uncertainty in Measurement (10). It establishes general rules for evaluating and expressing uncertainty in measurement across a broad spectrum of measurements. EURACHEM has produced an excellent document containing much more detail on how the concepts of the ISO guide can be applied in chemical measurement (4). The whole process of measurement uncertainty is schematically shown in Figure 5. The basic ideas are explained in this tutorial, but for more detailed information, readers are encouraged to study the EURACHEM document (4).
The concept of evaluating uncertainty is fairly straightforward. It requires a detailed knowledge of the nature of the measured and of the measurement method, rather than an in-depth understanding of statistics.

- Develop the specifications by writing a clear statement of exactly what is to be measured and the relationship between this and the parameters on which it depends. For example, if the measurement temperature has an influence on the result, the measurement temperature should also be defined.
- Develop a workflow diagram for the entire sampling, sample preparation, calibration, measurement, data evaluation and data transcription process (see Figure 1 for analytical sample testing).
- Identify and list sources of uncertainty for each part of the process or for each parameter. Possible sources for errors may be derived from non-representative sampling, operator bias, a wrongly calibrated instrument, lack of ideal measurement conditions, chemicals with impurities and errors in data evaluation.
- Estimate and document the size of each uncertainty, for example, as standard deviations or as RSDs. These data should be gathered from a series of measurements. Where experimental evaluation is impossible or impractical, the individual contributions should be estimated from whatever sources are available. Sources for this kind of estimation can be found in the supplier’s information or in the results of Interlaboratory studies or proficiency testing. The procedures and thoughts behind the way the contributions have been measured or estimated should be documented.
- Combine separate contributions in order to give an overall value. For example, where individual sources of uncertainty are independent, the overall uncertainty can be calculated as a multiple of the sum of squared contributing uncertainty components, all expressed as standard deviations. Computer software or spreadsheet programs can help to automate this calculation.
The whole procedure should be documented in such a way that sufficient information is available to allow the result to be reevaluated if new information or data become available. A complete documentation should include:
- A description of the methods used to calculate the measurement result and its uncertainty from the experimental measurements.
- The values and sources of all corrections.
- A list of all components of uncertainty with full documentation on how each of these was evaluated.
The expression of “Uncertainty in Measurements” is an integral component of the accreditation certificate being issued to the laboratories. Globalization of trade and technology implies the need for interchange ability of components, which must be produced with a high degree of exactness in measurement system. This concept is equally true for all other fundamental units of measurement. The International Bureau of Weights and Measures (BIPM), in consultation with various international bodies, have arrived at a new ISO standard on Expression of Uncertainty in Measurements, in 1995.
Measurement
What is a measurement?
A measurement tells us about a property of something. It might tell us how heavy an object is, or how hot, or how long it is. A measurement gives a number to that property. Measurements are always made using an instrument of some kind. Rulers, stopwatches, weighing scales, and thermometers are all measuring instruments.
The result of a measurement is normally in two parts: a number and a unit of measurement, e.g. ‘How long is it? ... 2 metres.’
What is not a measurement?
There are some processes that might seem to be measurements, but are not. For example, comparing two pieces of string to see which is longer is not really a measurement. Counting is not normally viewed as a measurement. Often, a test is not a measurement: tests normally lead to a ‘yes/no’ answer or a ‘pass/fail’ result. (However, measurements may be part of the process leading up to a test result.)
Uncertainty of measurement
What is uncertainty of measurement?
The uncertainty of a measurement tells us something about its quality. Uncertainty of measurement is the doubt that exists about the result of any measurement. You might think that well-made rulers, clocks and thermometers should be trustworthy, and give the right answers. But for every measurement - even the most careful - there is always a margin of doubt. In everyday speech, this might be expressed as ‘give or take’ ... e.g. a stick might be two metres long ‘give or take a centimetre.
Expressing uncertainty of measurement
Since there is always a margin of doubt about any measurement, we need to ask ‘How big is the margin?’ and ‘How bad is the doubt?’ Thus, two numbers are really needed in order to quantify an uncertainty. One is the width of the margin, or interval. The other is a confidence level, and states how sure we are that the ‘true value’ is within that margin.
For example:
We might say that the length of a certain stick measures 20 centimetres plus or minus 1 centimetre, at the 95 percent confidence level. This result could be written:20 cm ±1 cm, at a level of confidence of 95%. The statement says that we are 95 percent sure that the stick is between 19 centimetres and 21 centimetres long.
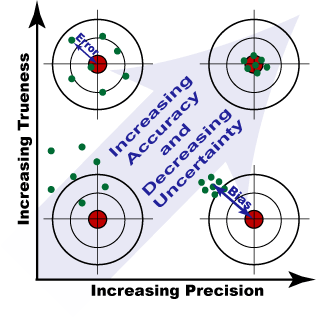
Error versus uncertainty
It is important not to confuse the terms ‘error’ and ‘uncertainty’.
- Error is the difference between the measured value and the ‘true value’ of the thing being measured.
- Uncertainty is a quantification of the doubt about the measurement result.
- Whenever possible we try to correct for any known errors: for example, by applying
- corrections from calibration certificates. But any error whose value we do not know is a source of uncertainty.
Why is uncertainty of measurement important?
You may be interested in uncertainty of measurement simply because you wish to make good quality measurements and to understand the results. However, there are other more particular reasons for thinking about measurement uncertainty.
You may be making the measurements as part of a:
- calibration - where the uncertainty of measurement must be reported on the certificate
- test - where the uncertainty of measurement is needed to determine a pass or fail or to meet a
- tolerance - where you need to know the uncertainty before you can decide whether the
- tolerance is met ... or you may need to read and understand a calibration certificate or a written specification for a test or measurement.
Where do errors and uncertainties come from?
Many things can undermine a measurement. Flaws in the measurement may be visible or invisible. Because real measurements are never made under perfect conditions, errors and uncertainties can come from:
- The measuring instrument - instruments can suffer from errors including bias, changes due to ageing, wear, or other kinds of drift, poor readability, noise (for electrical instruments) and many other problems.
- The item being measured - which may not be stable. (Imagine trying to measure the size of an ice cube in a warm room.)
- The measurement process - the measurement itself may be difficult to make. For example measuring the weight of small but lively animals presents particular difficulties in getting the subjects to co-operate.
- 'Imported' uncertainties - calibration of your instrument has an uncertainty which is then built into the uncertainty of the measurements you make. (But remember that the uncertainty due to not calibrating would be much worse.)
- Operator skill - some measurements depend on the skill and judgement of the operator. One person may be better than another at the delicate work of setting up a measurement, or at reading fine detail by eye. The use of an instrument such as a stopwatch depends on the reaction time of the operator. (But gross mistakes are a different matter and are not to be accounted for as uncertainties.)
- Sampling issues - the measurements you make must be properly representative of the process you are trying to assess. If you want to know the temperature at the work-bench, don’t measure it with a thermometer placed on the wall near an air conditioning outlet. If you are choosing samples from a production line for measurement, don’t always take the first ten made on a Monday morning.
- The environment - temperature, air pressure, humidity and many other conditions can affect the measuring instrument or the item being measured. Where the size and effect of an error are known (e.g. from a calibration certificate) a correction can be applied to the measurement result. But, in general, uncertainties from each of these sources, and from other sources, would be individual ‘inputs’ contributing to the overall uncertainty in the measurement.
The general kinds of uncertainty in any measurement
- The measuring instrument - instruments can suffer from errors including bias, changes due to ageing, wear, or other kinds of drift, poor readability, noise (for electrical instruments) and many other problems.
Random or systematic The effects that give rise to uncertainty in measurement can be either :
- random - where repeating the measurement gives a randomly different result. If so, the more measurements you make, and then average, the better estimate you generally can expect to get. or
- systematic - where the same influence affects the result for each of the repeated measurements (but you may not be able to tell). In this case, you learn nothing extra just by repeating measurements. Other methods are needed to estimate uncertainties due to systematic effects, e.g. different measurements, or calculations.
The two ways to estimate uncertainties
No matter what are the sources of your uncertainties, there are two approaches to estimating them: ‘Type A’ and ‘Type B’ evaluations. In most measurement situations, uncertainty evaluations of both types are needed.
- Type A evaluations - uncertainty estimates using statistics (usually from repeated readings)
- Type B evaluations - uncertainty estimates from any other information. This could be information from past experience of the measurements, from calibration certificates, manufacturer’s specifications, from calculations, from published information, and from common sense.
There is a temptation to think of ‘Type A’ as ‘random’ and ‘Type B’ as ‘systematic’, but this is not necessarily true.
Eight main steps to evaluating uncertainty
The main steps to evaluating the overall uncertainty of a measurement are as follows.
- Decide what you need to find out from your measurements. Decide what actual measurements and calculations are needed to produce the final result.
- Carry out the measurements needed.
- Estimate the uncertainty of each input quantity that feeds into the final result. Express all uncertainties in similar terms.
- Decide whether the errors of the input quantities are independent of each other. If you think not, then some extra calculations or information are needed. (See correlation in Section 7.3.)
- Calculate the result of your measurement (including any known corrections for things such as calibration).
- Find the combined standard uncertainty from all the individual aspects. (See Section 7.2.)
- Express the uncertainty in terms of a coverage factor (see Section 7.4), together with a size of the uncertainty interval, and state a level of confidence.
- Write down the measurement result and the uncertainty, and state how you got both of these.
How to reduce uncertainty in measurement
Always remember that it is usually as important to minimise uncertainties as it is to quantify them. There are some good practices which can help to reduce uncertainties in making measurements generally. A few recommendations are:
- Calibrate measuring instruments (or have them calibrated for you) and use the calibration corrections which are given on the certificate.
- Make corrections to compensate for any (other) errors you know about.
- Make your measurements traceable to national standards - by using calibrations which can be traced to national standards via an unbroken chain of measurements. You can place particular confidence in measurement traceability if the measurements are quality-assured through a measurement accreditation
- Choose the best measuring instruments, and use calibration facilities with the smallest uncertainties.
- Check measurements by repeating them, or by getting someone else to repeat them from time to time, or use other kinds of checks. Checking by a different method may be best of all.
- Check calculations, and where numbers are copied from one place to another, check this too.
- Use an uncertainty budget to identify the worst uncertainties, and address these.
- Be aware that in a successive chain of calibrations, the uncertainty increases at every step of the chain.
Send Enquiry !
Our Services
Our Clientele
The Logos are the property of the respective companies. There are use here just for the representation sake















